Siendo T el dominio del primer octante delimitado por las superficies y2 z=1, x2 z=1 Solución 1 6 RESOLUCIÓNLa intersección de ambas superficies en el primer octante seSea C la curva intersección de la esfera x2 y2 z2 =9 y el plano xz=3 (a)Utilizando el teorema de Stokes, transformar la integral de línea Z C ydxzdyxdz en una integral de superficie y hallar su valor (b)Verificar el resultado calculando directamente la integral curvilínea Solución 9p p 2 RESOLUCIÓN (a)La intersección de las superficies x2 y2 z2 =9 y xz=3 es la elipseC deY = x y x = 1 Solución Se tiene que la región D = (x;
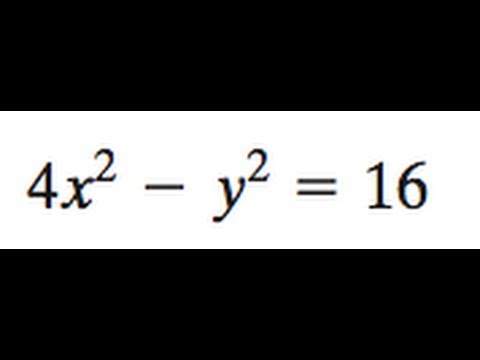
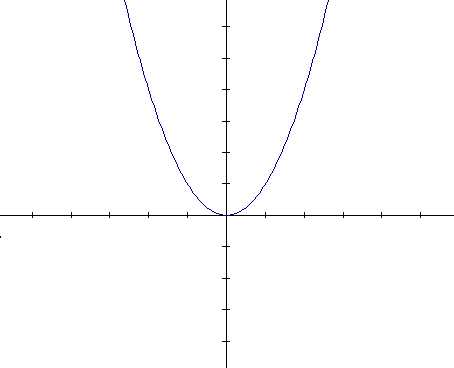
Hyperbola 4x 2 Y 2 16 Youtube
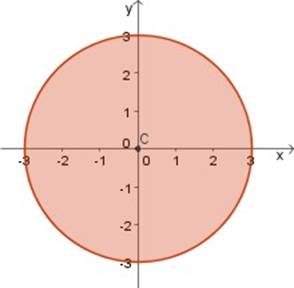
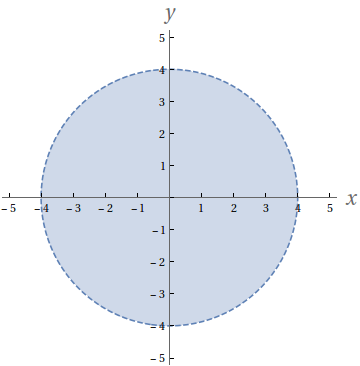
Grafica de la ecuacion x^2+y^2=16
Grafica de la ecuacion x^2+y^2=16-X2 y2 16 = 0 Hay curvas que se representan m as f acilmente mediante otro sistema de coordenadas por ejemplo, r= 2cos usando coordenadas polares Algunas curvas se describen mejor cuando las coordenadas x e y est an dadas en t erminos de una tercera variable t llamada par ametro x= f(t) e y= g(t), recordar las ecuaciones param etricas de una recta en el plano vistas en Grafica que corresponde ala ecuacion x2y2=16 2 Ver respuestas alexhuberth alexhuberth Respuesta paso a paso mendozamarc12 mendozamarc12 Explicación paso a paso Es la ecuación de una circunferencia ubicada en el origen y con radio 4 Si te parece, elijela como la mejor Saludos Nuevas preguntas de Matemáticas una bicicleta avanza con mru recorriendo 7



Obtener La Ecuacion De La Circunferencia Conocida Su Grafica
Calculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculoYdedensidad ˆ(x;y;z)=x2y2z2 Como kc0k= p 2,setieneque Sulongitudes L = R 2 ˇ 0 p 2 dt = 2ˇ p 2 ˇ Sumasaes M = R 2ˇ 0 (cos2tsen2tt ) dt = p 2 2ˇ8 3 ˇ 3 ˇ1258 Sudensidadmediaes,portanto 14 3 ˇ 2 ˇ142 g Sucentrodegravedad x = 1 M R 2ˇ 0 cost (1t2) p 2 dt = 6 34ˇ2 ˇ0014, y = 1 M R 2ˇ 0 sent (1t2) p 2dt = 6ˇ 34ˇ2 ˇ 044, z = 1 M R 2ˇ t (1t2) p(d) x = 2 no es una función La gráfica de x = 2 es una línea vertical Esto significa que en x = 2, y tiene muchos valores La gráfica se muestra a la derecha (e) x² y² = 16 no es una función Si x = 0, y² = 16 y y = 4 La gráfica es un círculo, similar a la figura (a) del problema 12 Un círculo no pasa la prueba de línea
(x 2 / 2) = 1 en esta región también está cercana a x 2 = a 2 De la misma forma puede observar que cerca del eje de las y, donde x es pequeña, la gráfica corta el eje en y=±b y su figura aparenta la de un círculo de radio b Un ejemplo Déjenme dibujar la elipse (x 2 /64) (y 2 /16) = 1Substitute 1 for a, 2x for b, and x^{2} for c in the quadratic formula, \frac{b±\sqrt{b^{2}4ac}}{2a} This equation is in standard form a x 2 b x c = 0 Substitute 1 for a, 2 x for b, and x 2 for c in the quadratic formula, 2 a − b ± b 2 − 4 a c y=\frac{2x±\sqrt{\left(2x\right)^{2}4x^{2}}}{2} y = 2 − 2 x ± (2 x) 2 − 4 x 2 Square 2x Square 2 x y=\frac{2x±\sqrt{4x^{2Dada la ecuación de la circunferencia(x2) (y5)=16 demuestra que el punto (36) es inferior a la circunferencia y que el punto (3,1) es exterior Ayuda por favor es urgente Responder Maria Noviembre Halla el radio y las coordenadas del centro de las circunferencias Luego, graficalas *(x2)2 (y5)2=raiz cuadrada de 7 Responder MARIA Noviembre Los extremos del diámetro
X2!3x 5 x 2 a > 0 x !R 4 Si ottengono altre funzioni usando • le 4 operazioni aritmetiche • la composizione funzionale (y=f(t) t=g(x) il dominio è degli x tali che g(x) appartenga al dominio di f) • l'inversione funzionale y=f(x) → x=g(y) (solo per funzioni biiettive) •Il legame tra due variabili x e y del tipo x2y2=16 non è una funzione (non è una funzione perché ad Como se grafica la ecuación x^2y^2=16 Recibe ahora mismo las respuestas que necesitas!X^2/9 y^2/16 = 1 Crea una Clase




Ecuacion De La Elipse Ejercicios Resueltos




Ejemplos Resueltos Circunferencia Y Elipse Pdf Free Download
Take the square root of both sides of the equation x^ {2}y^ {2}z^ {2}=0 Subtract z^ {2} from both sides y^ {2}x^ {2}z^ {2}=0 Quadratic equations like this one, with an x^ {2} term but no x term, can still be solved using the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}, once they are put in standard form ax^ {2}bxc=0Hemos desplazado la circunferencia x 2y 2=16 en los ejes, tal que x 0=1, e y 0=3 De esta forma la ecuación de la circunferencia será c (x1)2(y3)2=16 x2y 22x6y6=0 2) Sea la gráfica y=f(x)=x 2, la de una parábola con vértice en el origen Calcular la ecuación de la parábola con vértice en V(2,1) Hemos desplazado la parábola x 0=2, e y 0=1 Luego la nueva parábola será yY) 2 IR2 = 0 x 1;




Preguntero Matematica 2 Parcial 1 Y Algo De 2 Studocu
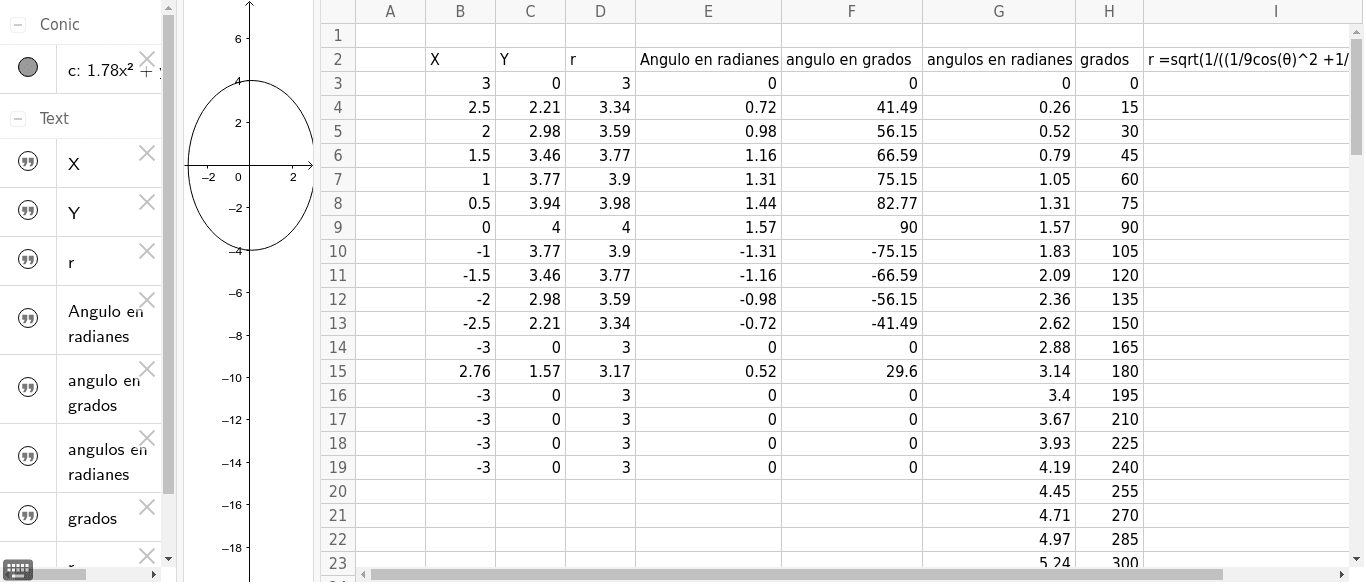



Elipse X 2 9 Y 2 16 1 Geogebra
La forma general de una superficie cuádrica es A x 2 B y 2 C z 2 D xy E xz F yz G x H y I z J = 0 Hay seis tipos básicos de superficies cuádricas elipsoide, hiperboloide de una hoja, hiperboloide de dos hojas, cono elíptico, paraboloide y paraboloide hiperbólicoX – 2 FIGURA 1524 Determinación de los límites de integración en coordenadas polares para la región del ejemplo 1 EJEMPLO 3 Evalúe donde R es la región semicircular acotada por el eje x y la curva (figura 1526) Solución En coordenadas cartesianas, la integral en cuestión es una integral fácil no elemen tal y no existe un modo directo para integrar con respecto a x o a y Sin'r' is a line specificationEach specification can include characters for the line color, style, and marker A marker is a symbol that appears at each plotted data point, such as a , o, or *For example, 'g*' requests a dotted green line with * markers Notice that the titles and labels that you defined for the first plot are no longer in the current figure window




Doc Taller N 13 Calculo Diferencial 1 Alejandra Pineros Academia Edu




Ejercicios 1 Ensenanza De Matematica Analisis Matematico
Z = x 2 y 2 < Hiperbolóide de uma folha x 2 y 2 z 2 = 1 < Helicóide (*) x = u cos v, y = u sen v, z = v < Catenóide (*) x = cosh v cos u, y = cosh v sen u, z = v < "Mola" (*) x = (11 2 cos u ) cos v, y = (11 2 cos u ) sen v, z = 2 sen u v < Gráfico da função (*) z = sen(x)cos(y)/5 3 cos(7W/4) exp(W)/2 onde W= (x p) 2 (y p) 2 < "Sela do Macaco" (*) z = x 3 3xy 2De esta manera la soluci on es x= 2 o x= 3 y ( 2;16) y (3;11) son puntos donde la tangente es perpendicular a y= 1 x 24 (ii)La tangente es paralela a la l nea y = p 2 12xcuando f0(x) = 12 6x2 6x 12 = 12 x2 x= 0 x(x 1) = 0, as x= 0 o x= 1 y los puntos donde la tangente es paralela a y= p 2 12xson (0;) y (1;7) 4Encontrar los maximos y m nimos de las funciones cuya gr a ca se muestra en lasJacque1102 jacque1102 Estadística y Cálculo Bachillerato contestada Como se grafica la ecuación x^2y^2=16 1 Ver respuesta jacque1102 está esperando tu ayuda Añade tu respuesta y gana puntos Polfed Polfed Como es una ecuación de circunferencias debes aplicar




Calculo En 2 Y 3 Variables Pdf Free Download



Funciones Transformacion De Funciones
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and Cónicas, Ecuaciones Paramétricas y Coordenadas Polares Santiago Bello CI Matemática III 2 Sección Cónica (Cónica) Sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano;Sa x2 y2 16 y x2 y x 2 x 0 x = 0 x2 y2 = 16 y = x2 y = x 2 Ahora hay que determinar a que´ parte de cada curva estan los´ puntos que satisfacen su restriccion´ Como tambien cumplen la con´ dicion de signo,´ x 0, concluimos que las soluciones factibles del problema son las que aparecen mas sombreadas en la fi´ gura De entre todas ellas, hemos de encontrar las que hacen que la




Obtener La Ecuacion De La Circunferencia Conocida Su Grafica
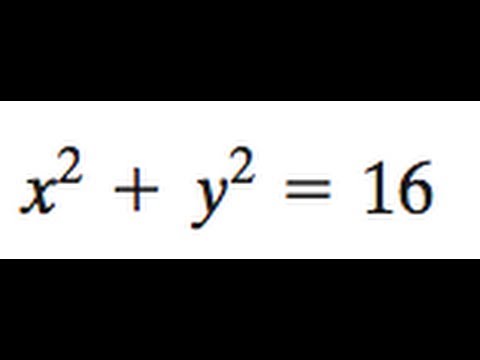



X 2 Y 2 16 Find The Foci And Vertices Of The Ellipse Youtube
Si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichasCalculadoras gratuitas paso por paso para álgebra, Trigonometría y cálculoGráfico x^2 (y2)^2=16 x2 (y − 2)2 = 16 x 2 (y 2) 2 = 16 Esta es la forma de un círculo Usa esta forma para determinar el centro y el radio del círculo




Graficos 3d Application Center



Ejercicios De Conicas
E sta p gina muestra varias superficies que son gr ficas de funciones de dos variables, es decir, son superficies generadas por una ecuaci n z=f (x,y) La gr fica de z=x2y2 es un paraboloide de revoluci n En la representaci n de la derecha se utilizan las ecuaciones param tricas x=2*u1 y=2*v1 z=x^2y^2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history Ejercicios Resueltos 1 Cálculo de integrales dobles en coordenadas rectángulares cartesianas 11 Problema Calcular ZZ D p x ydxdy si D es la región acotada por las respectivas rectas y = x;



Encuentra Aqui Informacion De Calculo De Volumenes Por Integracion Para Tu Escuela Entra Ya Rincon Del Vago




2 Dada La Ecuacion De La Descubre Como Resolverlo En Qanda
ò y 2 = 16 – x 2 ò x 2 y 2 = 4 2 (circunferencia) El recinto cuya área queremos calcular es medio círculo de radio 4 u 4 3 Área = = 1 1 π 42 = π r2 = 2 2 2 16 π = 8Se considera la super cie co nica x 2 y2 = z2 (z 0) Se pide 1 Calcular ela rea de la porci on de super cie co nica interior a la sup er cie esfe rica x 2 y2 z2 = 2 by (b > 0) 2 Calcular el centroide de Respuesta 3 Resolvemos el problema pordos procedimientos primero, proyect ando sobre el plano XY y segundo, parametrizando la super cie Primer m etodo 1 Calculamos losX0 x1 x2 xn−1 xn y0 1 y ym ym−1 Δ1 Δx2 n Δy1 Δy2 Δym # " Δxi Δy i yj R MOISES VILLENA Integración Múltiple 151 La ij ésima− partición tendrá forma rectangular Ahora cabe referirse al área de esta partición, que estaría dada por ΔAij i j=Δ Δxy Podemos definir una función de dos variables zfxy= (,) en la región R, que para la ij ésima− partición sería f (xy x



Dominios Curvas De Nivel E Esboco De Graficos Cursos




Numeros Fraccionarios Conceptos Y Terminos Fracciones Equivalentes Clases
Y = x/2, y = 2x (en realidad la region es union de dos regiones, una de ellas en el primer cuadrante y otra en el tercer cuadrante; Cual es la gráfica que corresponde a la ecuación x^2y^2=16 1 Ver respuesta andreainzunza39 está esperando tu ayuda Añade tu respuesta y gana puntos jhenifersita50 jhenifersita50 Esa es la gráfica con todo el procedimiento Nuevas preguntas de Baldor Si los numerales mostrados a continuación, están correctamente escritos 2n5(9) ^ 576n determine elLa fonction factoriser est en mesure de reconnaitre les polynomes du second degré et de les factoriser quand cela est possible Ainsi, la fonction permet de factoriser en ligne le polynôme du second degré suivant 6 x x 2, le résultat renvoyé par la fonction est l'expression factorisée (




Grafica Que Corresponde Ala Ecuacion X2 Y2 16 Brainly Lat




Evaluacion Parabola Derivado Rene Descartes
H 1 x 2 p 2 – y 2 q 2 = 1 H 2 – x 2 p 2 y 2 q 2 = 1 Gráficamente Cómo se aprecia en la gráfica las hipérbolas conjugadas tienen iguales asíntotas Ejemplo Dada la ecuación en R 2 A x 2 y 2 B y = 0 Hallar en cada caso, si es posible, los valores de A y B para que la ecuación dada represente a) Una elipseSUSCRÍBETE http//bitly/VN7586 (NO OLVIDES DAR UN ¨LIKE¨)VISITA http//math2mecomFB http//bitly/FBmath2meG http//googlecom/math2meTwitter http/Planoscoordenadosconelplanoxy (z = 0)eslarectay = x 2,conelplanoyz (x = 0) eslarecta z = y2 ,yconelplano xz ( y = 0 )es z = x2 Conestainformaciónpodemos esbozarlagráficade f comoseveenlaFigura32




Hiperbolas Con Centro En H K Ck 12 Foundation




1 Dada La Ecuacin Dela El Lihat Cara Penyelesaian Di Qanda
Igualar y y al nuevo lado derecho Use la forma de vértice, y = a ( x − h) 2 k y = a ( x h) 2 k para determinar los valores de a a, h h, y k k Dado que el valor de a a es positivo, la parábola se abre hacia arriba Encuentra el vértice ( h, k) ( h, k) Hallar p p, la distancia desde el vértice al focoGrafica las seis funciones trigonométricas seno, coseno, tangente, cotangente, secante y cosecante Identifica en una gráfica la amplitud, el período, la frecuencia y el desfasamiento Incorpora a sus actividades educativas y cotidianas las telecomunicaciones y los sistemas de información ( MANEJO TECNOLÓGICO) Maneja efectivamente los principales instrumentos y Límites y continuidad de un campo escalar Observaciones (1) Como en el caso de los campos centrales, casi todos los campos que aparecen en la práctica se obtienen aplicando a un polinomio en varias variables las operaciones habituales suma, resta, multiplicación y división y las funciones elementales de una variable (potencias, raíces, exponenciales, logaritmos, funciones
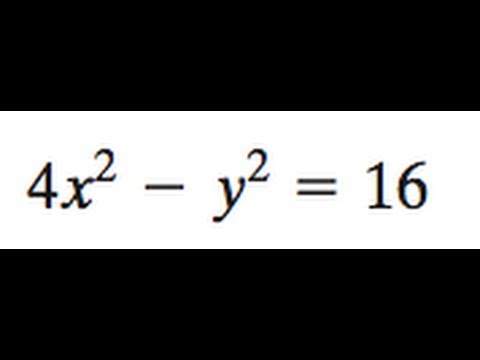



Hyperbola 4x 2 Y 2 16 Youtube




Introduccion Matematicas 04 Studocu
INTEGRACIÓN MÚLTIPLE INTEGRALES TRIPLES 1/18 1Problema 1 Calcular ZZZ T zdxdydz;X^2 y^2 = 16 find the foci and vertices of the ellipseSo I got a circle, $1=x^2 y^2$ But when I eq Stack Exchange Network Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange Loading 0 0;




2 Maneras De Representar Graficamente Una Circle Para Dummies
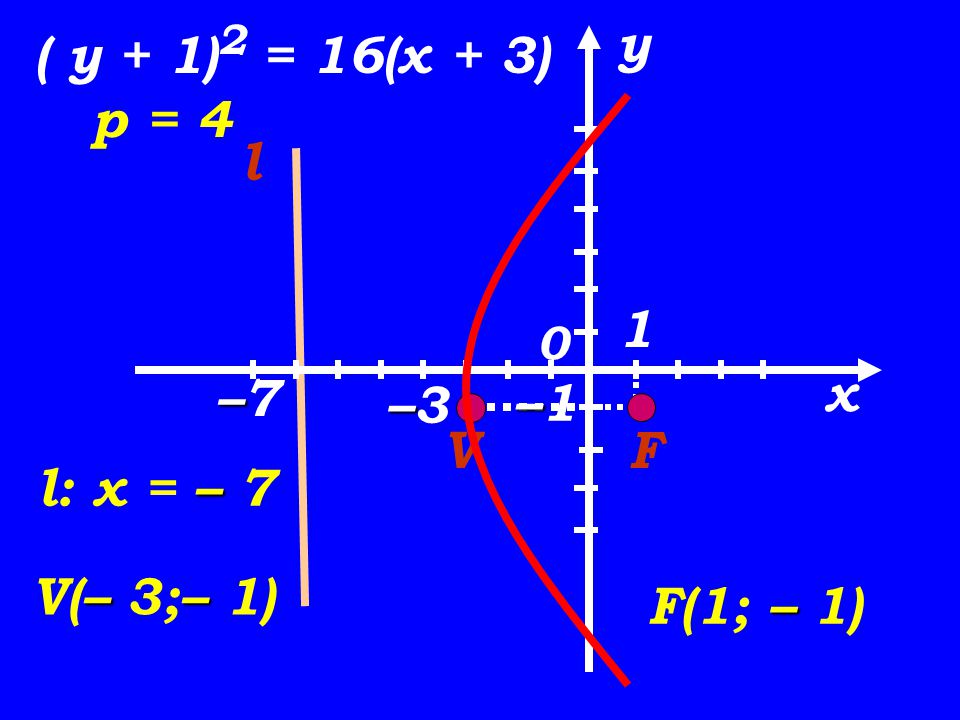



Clase 180 Ejercicios Sobre La Ecuacion De La Parabola F V L Y2 4px Ppt Descargar
642 Capítulo 11 Ecuaciones paramétricas y coordenadas polares (f(b), g(b)) es el punto ˜nalCuando tenemos ecuaciones paramétricas y un intervalo para el parámetro de la curva, se dice que hemos parametrizado la curvaLas ecuaciones y el intervalo, en conjunto, constituyen la parametrización de la curva Una curva determinaTour Start here for a quick overview of the site Help Center DetailedX y x ZZ D p x ydxdy = Z 1 0 Z x x p x ydydx = 2 3 Z 1 0 (x y) 3=2 x x
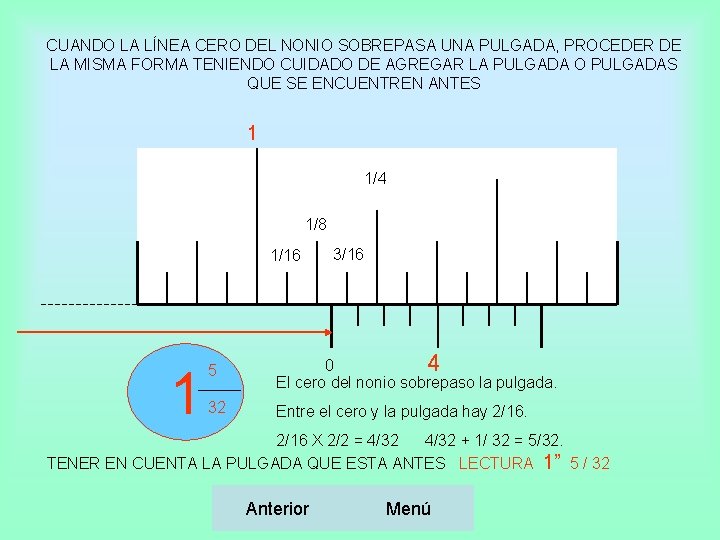



Medicin Efectuar Una Medicin Significa Comparar La Distancia




10 Sea Q La Region Limitada Por La Esfera X2 Y2 Chegg Com
(x4)^2 (y4)^2 = 5 x^2 y^2 = 16 a) Use el enfoque gráfico para obtener los valores iniciales b) Encuentre aproximaciones refinadas con el Método de NewtonRaphson Rúbrica literal a (10 puntos), literal b ( puntos)Z Z R (12 3x 2y)dA= 95 2 4 Calcular RR D (x 2 y)dAsiendo Dla región comprendida entre las grá cas de las curvas y= x2, y= x2 y las rectas x= 2 y x= 2 Se tiene Z Z D (x2 y)dA= Z 2 2 Z x2 x2 (x2 y)dydx= Z 2 2 x2y y2=2 x2 2x dx= = Z 2 2 2x4 dx= 2x5=52 2 = 128=5 5 Determinar RR D xydAsiendo Dla región del primer cuadrante ence(x3) 2 y 2 = 16 x 2 (y3) 2 = 16 s Question 6 SURVEY 300 seconds Q Si a la circunferencia dada por x 2 y 2 = 16 se le aplica una traslación, de modo que su centro se ubique en el I cuadrante y que ambos ejes de coordenadas sean tangentes a esa circunferencia, entonces la ecuación para esta circunferencia corresponde a answer choices (x4) 2 (y4) 2 =16 (x4) 2




Graficar Calcular Superficie




Graficos 3d Application Center
This preview shows page 415 422 out of 4 pages 18 La gráfica de la ecuación 4 x 29 y 216 x 18 y 43 = 0 está dada por26 Acotado por el cilíndro y^2z^2=4 y los planos x=2y, x00, z=0 en el primer octante 27 Acotado por el cilíndro x^2y^2=1 y los planos y=z,x=0,z=0 en el primer octanteComo las regiones tienen la misma area y la funci´on z = x 2 y es sim´etrica, bastar´a multiplicar por dos el resultado obtenido al considerar un´ icamente la parte del primer cuadrante) z 4 Podemos pues escribir el volumen como V = 2 ZZ R dxdy Z x2y2 0




10 3 Evaluar Y Graficar Funciones Exponenciales Las Matematicas




Graficos 3d Application Center
Ii) f(x,y) = x2 y2, D recinto limitado por y = x2, x = 2, y = 1 iii) f(x,y) = x 2y, D es el primer cuadrante del c´ırculo x y2 ≤ 4 iv) f(x,y) = y, D = {(x,y) y > 0, x2 y2 ≤ a2, y2 ≥ 2ax, x ≥ 0} Solucion´ i) Los puntos de interseccion de las curvas y = senx, y = 2x/π son (0,0) y (π/2,1) La integral se calcula entonces de
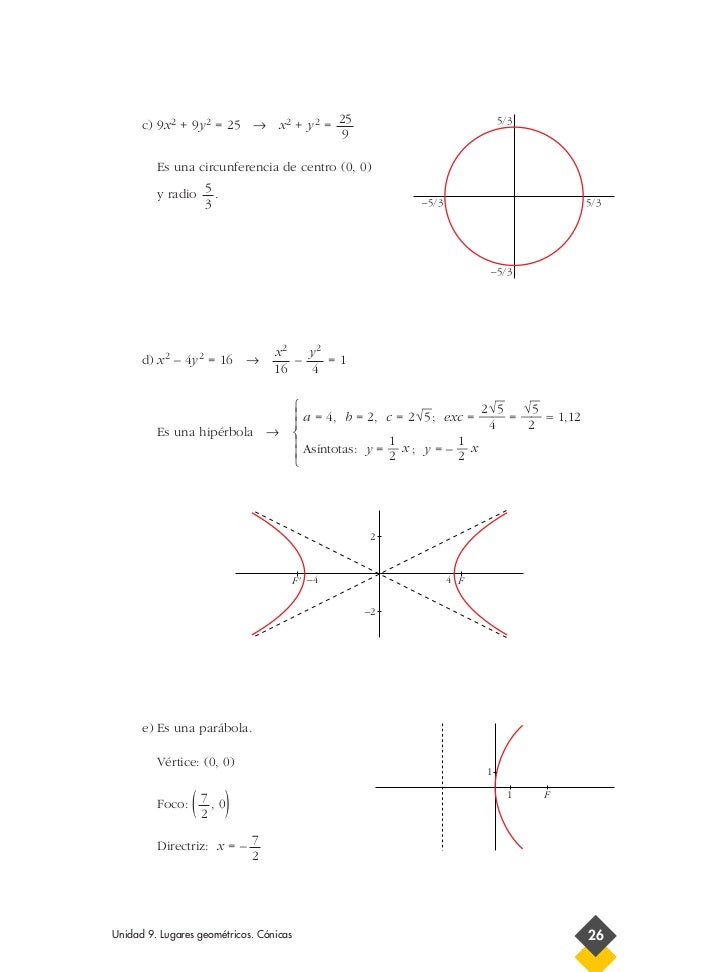



Soluciones Conicas
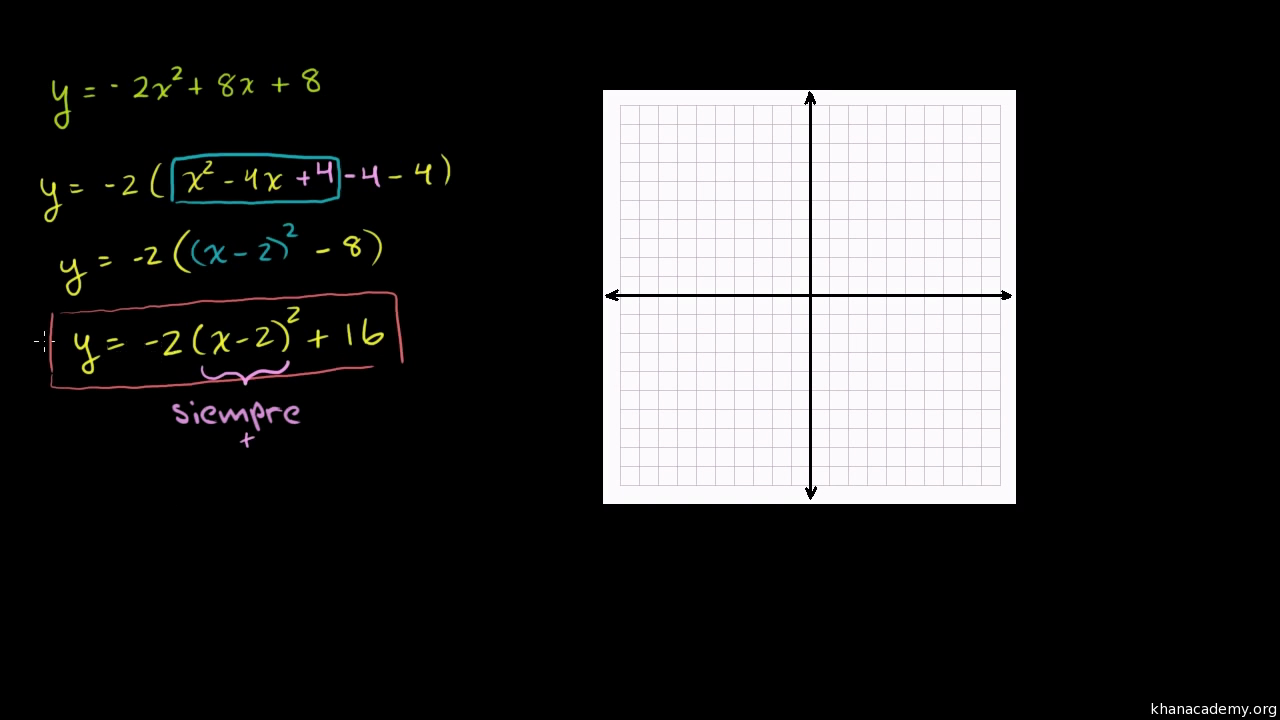



Vertice Y Eje De Simetria De Una Parabola Video Khan Academy
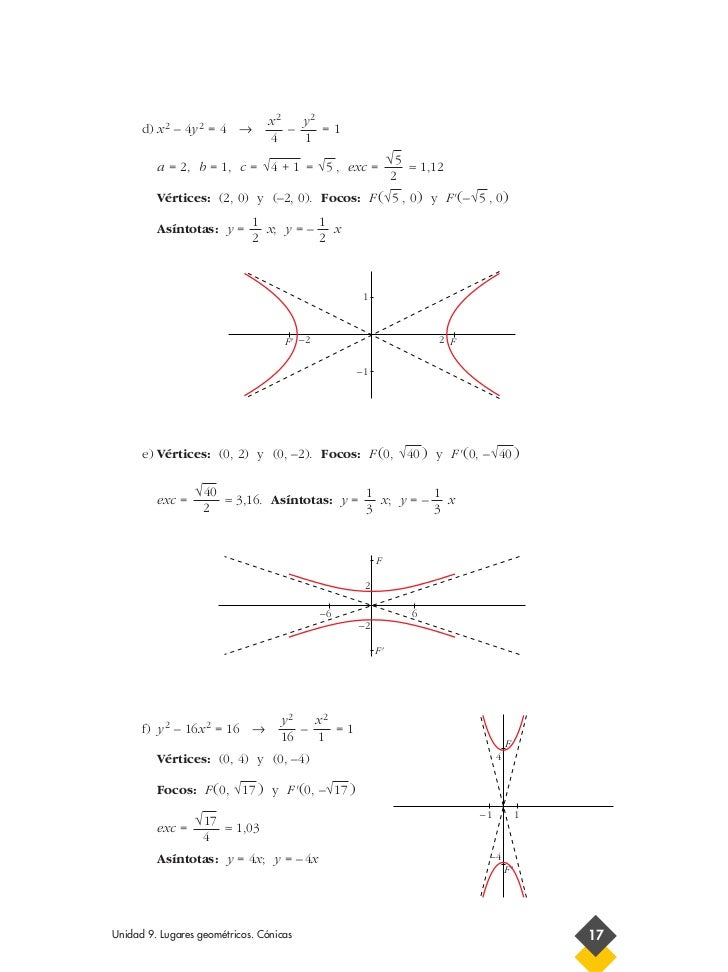



Soluciones Conicas



Www Webcolegios Com File 4bc162 Pdf




Pdf Exponencial Y Logaritmos Jhomaira Burbano Academia Edu




Matemauro Ecuaciones Canonicas Facebook




Graficar Y Realizar La Ecuacion Cuadratica C Y X2 16 Brainly Lat
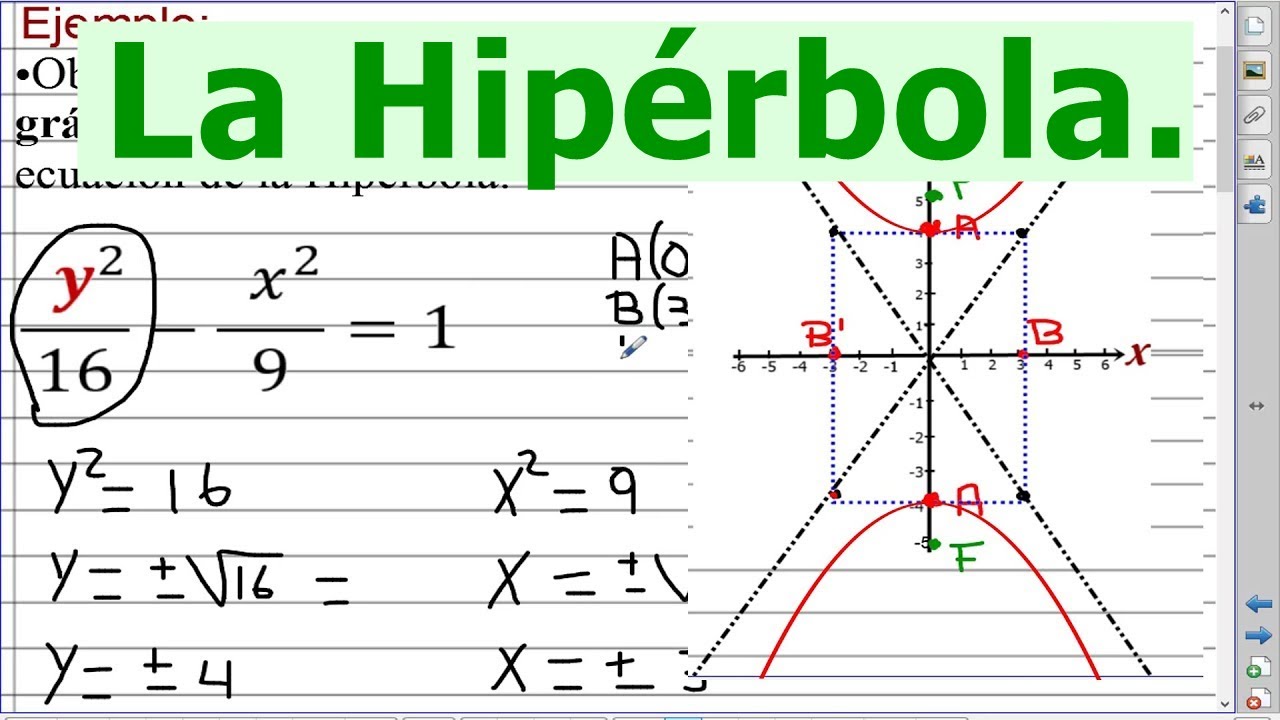



Dada La Ec Y2 16 X2 9 1 Hallar Vertices Focos Longitud De Los Ejes Grafica Ec De Asintotas Youtube



El Sapo Sabio 11 Julio




Que Lugar Geometrico Modela La Siguiente Ecuacion X 6 16 Y 2 Brainly Lat



Graphing Linear Inequalities



Graficar Calcular Superficie



Graficar Calcular Superficie




Matematica Y Fisica La Diversion Del Tiempo Libre




Funciones Cuadraticas




69 Que Grafica Corresponde A La Ecuacionx 2 16 Y Y 2 25 1 Brainly Lat




Grafica De 0 3 2 X E X Download Scientific Diagram




More On Hyperbolas




Ecuaciones De La Circunferencia Geogebra




Sociales Y Administrativas La See How To Solve It At Qanda




Calameo Ejercicios Parabola 19b




Ejercicios De Circunferencia Docsity




Suma Y Multiplicacion Algebraica Leyes De Exponentes Ecuaciones Geometria




Circunferencia Victor Ibanez Academia Edu
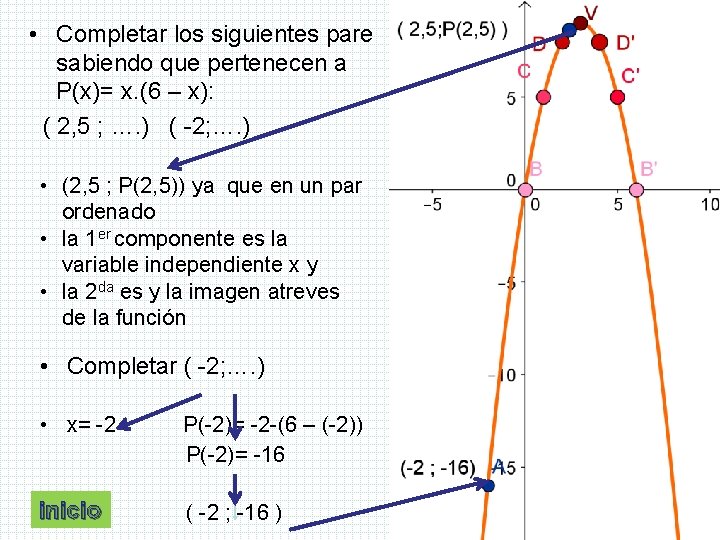



Funcin Cuadratica Parbola Temario Funcin Cuadrtica Definicin Situacin




Grafica Del Elipsoide X 2 4 Y 2 9 Z 2 25 1 Funcion De Dos Variables Youtube



Calculo Ecuacion De La Tangente A Un Circulo Dado La




Ejercicios De La Funcion Lineal Superprof



Graphing Linear Inequalities




Agregar Descripciones De Texto A Puntos De Datos Matlab Text Mathworks Espana




Graficos 3d Application Center




Soluciones Integral Definida By Jose Antonio Tarifa Garzon Issuu



Graficar Funciones Raiz Cuadrada




Cual Es La Grafica Que Corresponde A La Ecuacion X 2 Y 2 16 Youtube



Altura Alcanzada Por Un Proyectil Es De F X 16x 2x 2 Donde Y Es




Ejercicios De Graficas Y Funciones Superprof



Www Menvill Edu Mx App Download S3 Ga Geometr C3 Ada Anal C3 Adtica Pdf T




Ecuacion De La Circunferencia Ejercicios Resueltos Pdf




Determinar El Centro Y El Radio Y Escribir Una Ecuacion De La Circunferencia Que Pasa Por Tres Puntos Ejercicios De Matematica



Www Menvill Edu Mx App Download S3 Ga Geometr C3 Ada Anal C3 Adtica Pdf T




Ejercicios De La Ecuacion De La Parabola Superprof
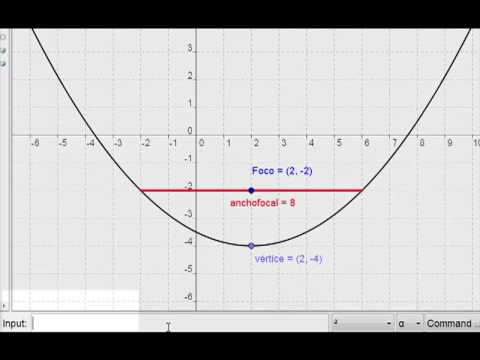



Parabola X 2 2 8 Y 4 Youtube




Percentage Of Maturity Stages Holden And Raitt Scale Of Females Of Download Scientific Diagram




Resolucion De Sistemas De Ecuaciones Por Medio De Graficas Articulo Khan Academy




Calameo Circunferencia




1 Determina Las Coordenadas D See How To Solve It At Qanda



Graficar Calcular Superficie
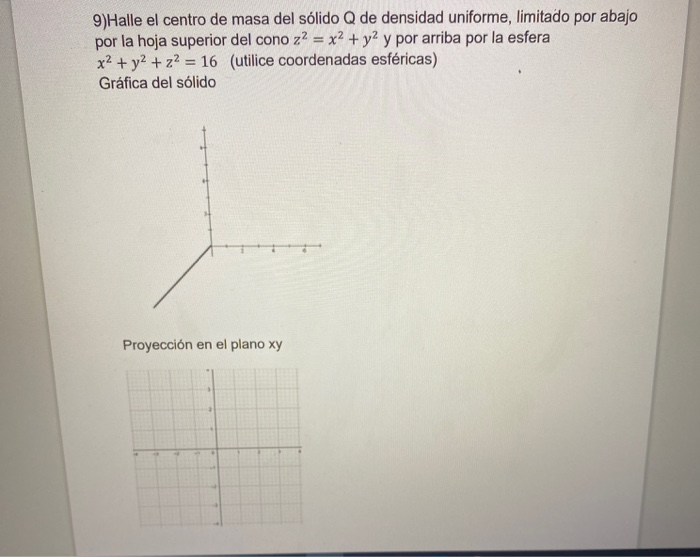



Halle El Centro De Masa Del Solido Q De Densidad Chegg Com




Volumen Solidos Ejercicios Volumenes Solidos Con Aplicacion Docsity




Cual Es La Grafica Que Corresponde A La Ecuacion X Y 16 Brainly Lat




Grafica De La Funcion F X 16 X Brainly Lat




Hallar El Volumen Del Solido Generado Al Rotar Alrededor Del Eje Y La Region Acotada Por La Curva Brainly Lat




Graficos 3d Application Center




Anailisis Matematico Iii Fabiola Integral Colector




Grafico Di Un Quadrato Sotto Radice Quadrata




Taller De Conicas Para Explicar En Clase By Duban Duque Issuu




Ecuacion De La Elipse Ejercicios Resueltos
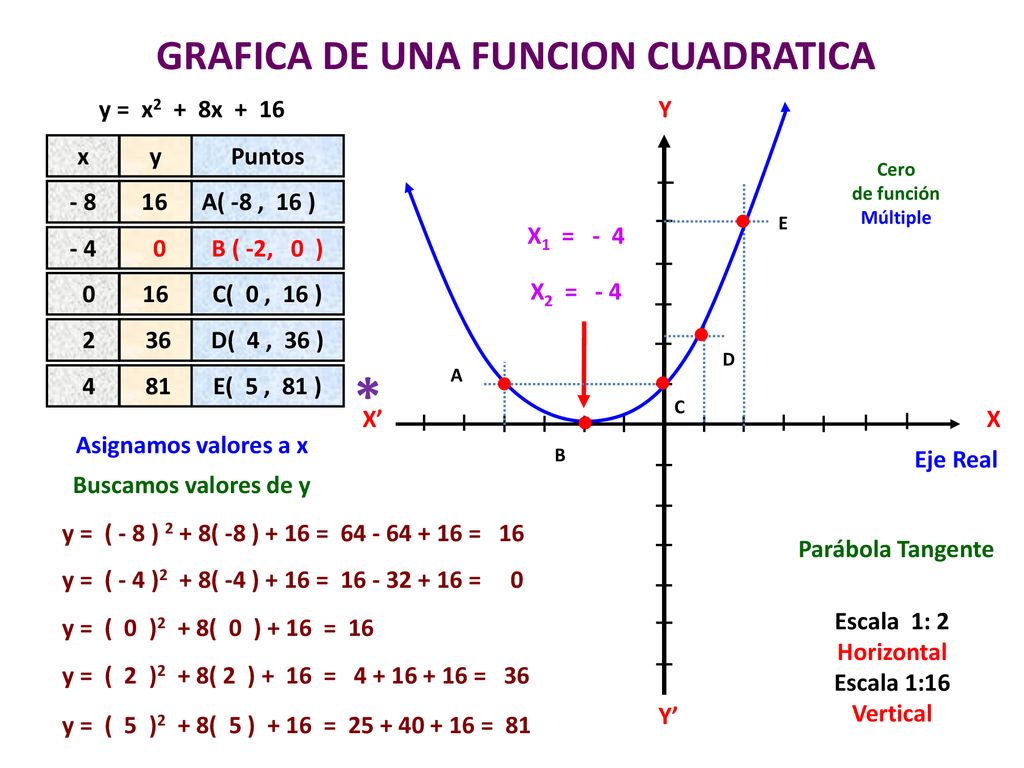



Formula General Ppt Descargar
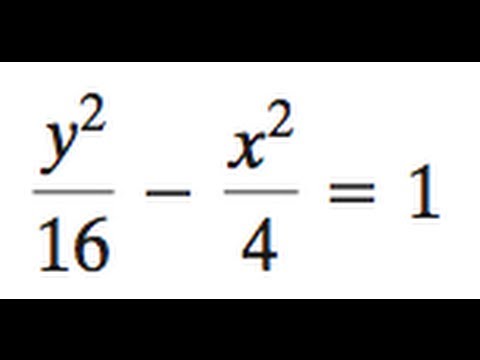



Hyperbola Y 2 16 X 2 4 1 Youtube




Graficando Desigualdades Lineales




25 Noviembre 13 Sobre Todo Matematicas




A02q Sem01 Ses02 Parabola Separata Objetos Matematicos Objetos Geometricos



Halla El Centro Y El Radio De La Circunferencia X 2 Y 2 8y 0



Graficar Calcular Superficie




Elipse Ejercicios Resueltos



Superficies Cuadraticas




G X 2 2z 2 8 H Z 2 X 2 Y 2 1 I X Z 2 Y 2 Pdf Free Download




Matematica Y Fisica La Diversion Del Tiempo Libre




Ejercicios De La Funcion Lineal Superprof



Http Www Mate Unlp Edu Ar Practicas 54 5 Pdf



0 件のコメント:
コメントを投稿